Noise Helps Signal Detection
Surface nuclear magnetic resonance (SNMR) is one of the most precious signals in the world of hydrogeophysics. Precious in terms of the information it contains, but also in its intrinsic fragility. The surface NMR signal is often swamped by interference from powerlines and even electromagnetic radiation from far off lightning storms. Even after many years, when I see a water signal in surface NMR measurement, I’m still in awe that it works.
The question is what are the limits on surface NMR ability to detect water? For a long time, I believed the answer depended on how finely we discretize our analogue signal; the resolution of the bit determines the smallest possible signal we can measure. My rational for this belief was that if the NMR signal is not large enough to change the value of the measured bit, we could not observe the oscillator nature of the NMR signal and therefore we would not detect its presence. If we take a noise-free signal, discretize it, if the signal amplitude is always below 1/2 the bit resolution, the digitized signal will be a stream of zeros. No detected signal. But, my supervisor, wisely postulated that the presence of noise means this is not the fundamental limit on a signal detectibility. This does not match my intuition. Can adding noise actually improve a signals detectibility? This is the inspiration for this post. Let’s look at some simulations.
To start we’ll check the noise-free case, discretizing a signal.
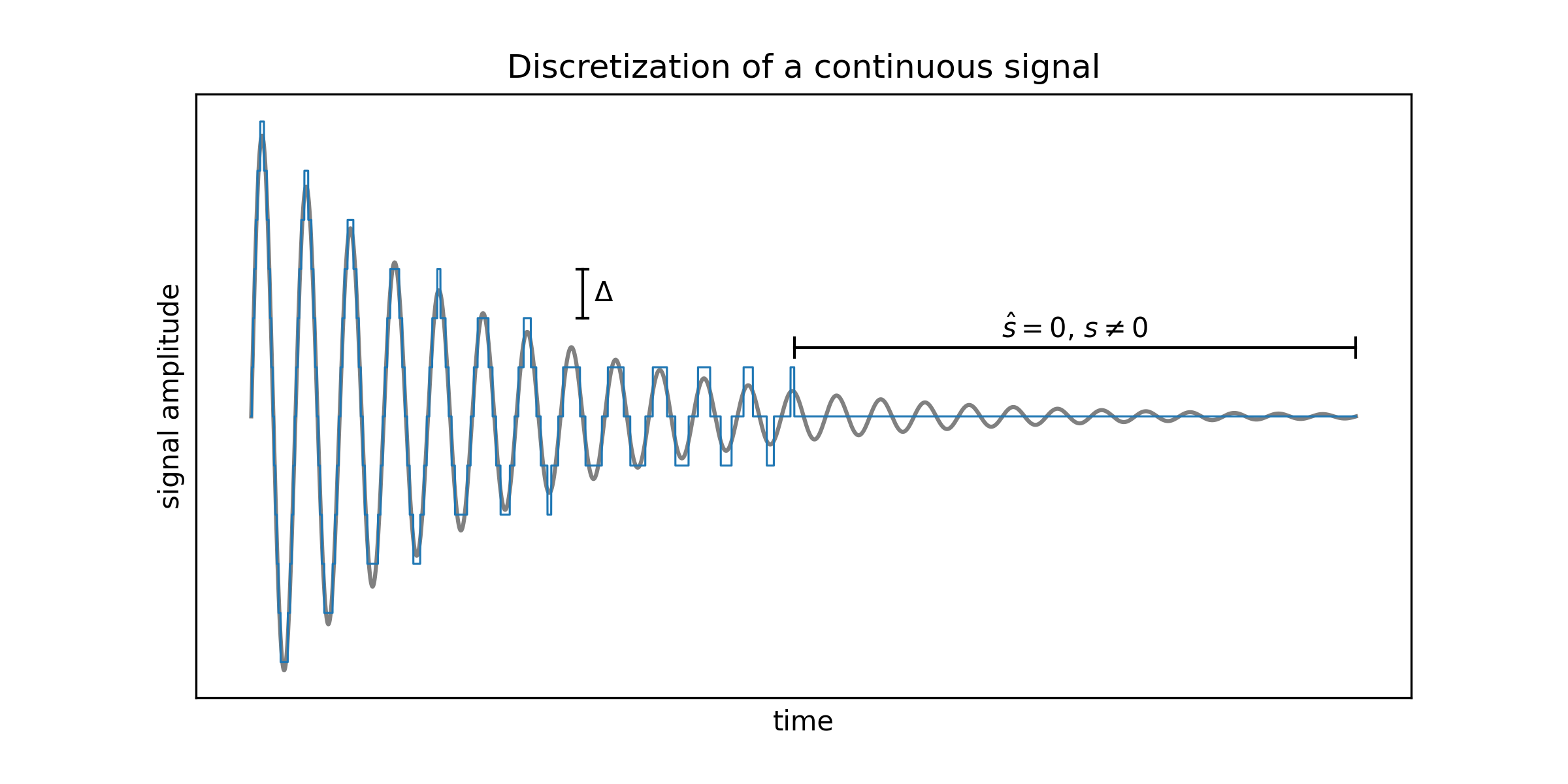
Figure 1: A discretized exponential decay.
In the background we see an idealized surface NMR signal; a single frequency oscillation with an exponentially decaying envelope. Setting the bit resolution to $\Delta$, we see the more staircase-like nature of the digitized signal in blue. Here we confirm our intuition; when the signal amplitude is always below 1/2 the bit resolution, the digitized signal is a stream of zeros. No detected signal for the second half of this noise-free recording.
Now lets add a little noise to the signal before we discretize it. This will represent a single measurement or ‘stack’ in the field. Of course it becomes much more difficult to see the underlying signal. To mimic our operations in the field, we will repeat the measurements 10-100s of times and take the average to reduce the noise effects. Let’s try with 100 repeats to see the its effect.
Figure 2: the addition of noise on the signal and the effects of averaging repeated measurements.
It’s impressive how averaging the signal can salvage the underlying signal in the midst of such high noise levels. A big W for stacking.
Now having seen the effects of the discretization, added noise, and signal averaging, we’ll analyze the signal more carefully. Since the signal has a very particular frequency, analyzing it’s frequency content Fast Fourier Transform (FFT) is a natural approach.
Figure 3: FFT of previous signals.
To my surprise the FFT of the discretized signal closely match that of the continuous signal. The effects of discretizing really only effect the high frequencies.
- sidenote: applying a window to a signal (for example, zeroing out the pulses) means that no matter what amplitudes are present in this interval, the result will be zero there. Looking at this in the frequency domain, the convolution with the window spectra still results in this zeroed interval in the time-domain.